In the simplest terms, the modulus of elasticity (MOE) measures a wood’s stiffness, and is a good overall indicator of its strength.
Technically it’s a measurement of the ratio of stress placed upon the wood compared to the strain (deformation) that the wood exhibits along its length. MOE is expressed in pounds-force per square inch (lbf/in2) or gigapascals (GPa). This number is given for wood that has been dried to a 12% moisture content, unless otherwise noted.
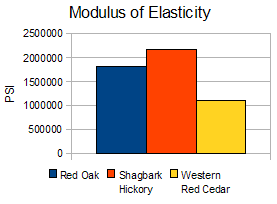
In practical terms, the number itself isn’t all that meaningful, but it becomes useful to use in comparison with other woods. For instance, Hickory is known to have excellent strength properties among domestic species in the US, and has a MOE of 2,160,000 lbf/in2 (14.90 GPa). In comparison, Red Oak is another well-known wood used in cabinetry and furniture, and has a MOE of 1,820,000 lbf/in2 (12.50 GPa).
Get the hard copy
If you’re interested in getting all that makes The Wood Database unique distilled into a single, real-world resource, there’s the book that’s based on the website—the Amazon.com best-seller, WOOD! Identifying and Using Hundreds of Woods Worldwide. It contains many of the most popular articles found on this website, as well as hundreds of wood profiles—laid out with the same clarity and convenience of the website—packaged in a shop-friendly hardcover book.
do you have references for where you get your MOE data in your book?
Yes and no. All my sources are listed in the Bibliography, but I don’t give sources for each individual species/data point in the book.
Seems to be a lot of questions about modulus of elasticity aka Young ‘s modulus. This constant as stated reflects the stiffness (resistance to deflection) of a material under a load but only in its elastic range, the relatively small range in which it springs back without any deformation after the load is removed. With wood this springy range is much wider than other materials say a sheet of glass, but almost anything can have its MOE determined. With common engineering materials this figure is so important that huge amounts of testing have been done to determine the MOE/Youngs modulus… Read more »
What I find interesting is how the MOR can be lower than the MOE. How can you measure the elasticity of a wood if it will break before you see a bending? Look at the https://www.wood-database.com/rhodesian-teak/ for instance. The MOR occurs at a much much lower force than the MOE.
I will assume that I am misunderstanding something here.
I was also confused by this. The MOE is a measure of the amount a material changes shape is some dimension (be that stretching, compressing, or bending) under a stress that does not exceed the material’s elastic range (i.e. the point where the material won’t spring back to is original shape). This produces a ratio (unlike the MOR which is a direct measure of the force necessary to produce failure) but the ratio is “hidden” because the units measuring the deformation are cancelled out in the equation. To address your specific question, the MOE can be (and often is) bigger… Read more »
yes, I think I udnerstand it now. I had to discuss this with my mechanical engineer colleague. So basically the MOR starts counting once the material has gone from elastic to plastic. The MoE is the force measured just until plasticity, which as you say takes a higher force than the force to rupture the plasticity in the material. So the question then is. Which one is the best measure for a woods true strength? For instance, if you want the strongest axe shaft to your large firewood splitter, should you go with a wood with higher MOE vs MOR… Read more »
If there are any structural engineers on this thread, please chime in but, as I understand it, MOE is a good measure of a wood’s strength *relative* to other woods and would be a good place to narrow down woods choices for active applications like a hammer or axe handle. MOR is an *absolute* measure of a wood’s maximum load before failure and therefore would be a useful data point for wood to be used in building applications when used in conjunction with the MOE. Yellow pine would not be a suitable axe handle but it’s high strength combined with… Read more »
Just note that in testing MOE, the load is applied gradually, so it doesn’t directly equate to something like a hammer blow or a swing from an axe. There are other, more specialized tests that are used to measure a wood’s impact resistance, which don’t always correlate strongly to its MOE.
That makes all the difference according to my knowledge in engineering. The instantaneous blow in force probably makes the MOR slightly more relevant. A lot of axe shafts rupture mainly due to grain run out in the shafts. So that is by definition a rupture that occurs. Which evidently has a much lower resistance to force when grains are not aligned as straight as possible from the bottom of the handle to the top of the axe head (eye). According to the science on Britannica https://www.britannica.com/science/wood-plant-tissue/Hygroscopicity the best measure of a woods strength is the density, but as you Eric… Read more »
How does one use modulus of elasticity to select wood to make a bow (as in bow and arrow) and/or the frame of a canoe? Thank you
In either case you’d want to stay well within your outer limits. Module of rupture is useful to know as well. That’s the point at which you’d get fracturing in the grain. With a canoe working within the modulus of rupture would be fine since it will remain in the same shape. Module of rupture doesn’t account for fatigue though. Bend a board to much and it may not break but it won’t necessarily spring back to its original shape. So with a bow modulus of elasticity is what you’re looking for since that’s the limit you can bend it… Read more »
I am curious to better understand exactly how the values and units translate into real world measurable terms. That is, we understand that crushing strength in psi is the force in pounds to crush a one square inch block of wood, and the tensile strength would be how many pounds a one square inch section could hold if we cold hang that weight from it. This MOE is giving us forces in millions of lbs per square inch. what exactly would that look like in a test?
Carroll It doesn’t look like anything unfortunately. It is only after you combine this value “E” with geometric dimensional properties of the element being loaded or designed that you can compute a relationship between load and deflection (movement). For example, a simple expression of the shortening of a column under load would be delta = P*L / (E*A). This is saying the column gets shorter by an amount delta equal to the product of the load (P) and the length (L) of the column divided by the product of the modulus (E) and the area (A). So in this example… Read more »
1. I’m curious what sources you use for the modulus of elasticity? 2. From your diagram, it appears you are actually talking about the flexural modulus, which may or may not be equivalent to the tensile modulus or the compressive modulus, depending on the material. For wood, I don’t know if they are the same or different. Perhaps you do? https://en.wikipedia.org/wiki/Flexural_modulus I think the flexural modulus also depends on the orientation of the grain, radial or tangential, to the force. For example, a quater-sawn guitar neck is much stiffer then one made from plain-sawn wood. Perhaps you could specify which… Read more »
As we all know, Wood is anisotropic, therefore strength is highly dependent on relative direction of the grain.
Use MOE with caution and keep in mind that Wood is stronger along the grain than across it.
Vastly more resources would need to be put into wood research in order to make a moderately accurate information data base of wood rigidity among the many variables found in nature. I go with generalities and overdesign.
How can I buy your WOOD book. I have searched Amazon for book entitled WOOD and no luck?
This page has a link to buy the book: https://www.wood-database.com/book/
The thing that folks miss here is that in using Youngs modulus with say metals the general assumption is that it is the same in tensile stress as in compressive stress. With wood this is definitely not the case. So in a wooden beam under load the modulus on the tension side of the beam is not the same as in the compression side. Hence difficult to analyse.
There are at least 2 reasons there are different published values for E for the same named wood and neither has to do with compression or tension of the wood fibers. 1. The Modulus of Elasticity published in many texts in the past was based on bending tests instead of opposing shear forces used in modern testing procedures. The bending test didn’t consider or compute either tension or compression in determining the value for E. The formula used the applied force, the span, the moment of inertia, and the deflection in a formula that is available in many older texts… Read more »
This article says red oak “has a MOE of 1,820,000 lbf/in2 (12.50 GPa)”, but looking at the database page for red oak I find, “Elastic Modulus: 1,761,000 lbf/in2 (12.14 GPa)”
Why the discrepancy?
The short answer is that I use the average of as many credible sources of data that I can find, and when this article was written, I was quoting from only one source, while the page on red oak has since been updated to reflect the most recent (averaged) data.
You can hear a little bit more of my rationale in determining values to list on the website in this longer video: https://www.youtube.com/watch?v=IfXW9Tw-3O0
1.76 and 1.82 is not a discrepancy. Those are good values to use. Woods actually vary a lot more than that. It is not like you are testing a mill run of SAE 1035 steel, or something. Wood varies in the same species by geographical location. It also varies by altitude in the same location. Scots pines at sea level to 500 feet are soft and weak. If you go a mile on up that same hill to 2,500 to 3,000 feet, it is 50% more dense than the sea level wood, whether green or oven dried to the same… Read more »
“1.76 and 1.82 is not a discrepancy.”
Actually, it is a discrepancy. Perhaps you meant to say it is not a large difference. If so, I would agree with that. But it is most definitely a discrepancy in the database. Even 1.80 and 1.81 would be a discrepancy. A reference should not give different values for the same thing. Now, if the reference had quoted a range (the same range both times), that would be fine. But giving two different numbers for the same thing is a discrepancy.
It is indeed amazing that this should be so – truly a correct use of the word, rather than the ‘Amaaaazing’ that vocabulary-poor Americans (and now, and aping them, Europeans too) use to describe every observation they make that is on the positive side of neutral.
And it’s also amazing that Stradivarius and Guarnerius must have, without instruments, been able to appreciate the subtleties of this variation when selecting trees from which to make their violins.
Hang a weight from steel wire; say 1 pound. This weight acts under gravity to deform this wire along its length. The force is pure Tensile Force. intial length divided by change length gives strain. Young’s mod is then calculated based on the force (weight times acceleration due to gravity) and area of the wire. It can be clearly seen in the above woods database diagram, that a system of compression and tension is happening. The true lengthwise deformation would be given by Pythagoras. If the E value is to have any meaning, it would also mean that if we… Read more »
There is huge confusion in calculating MOE in Plywood please help us is there is any other method to calculate the said parameter Unit= N/mm2
Awesome information and nice with everyone sharing comments trying to explain the modulus of elasticity. It makes it possible to read different explanations. This page is and will help me through my woodscience course. 5/5 Pine cones.
MOE is the ration between the stress and the (non-dimensional) relative elongation. If this ratio is 1/1000 (the material lengthens or shortens 1 mm for each meter), then the ratio gives 1000 more that stress, in the same units as yield or crush limit MOR.
Hello
I am attempting to calculate whether a particular timber section (say C16 grade) will be strong enough, i.e. will not snap, under the wind load, and also the deflection at its tip. Can anyone help me with the formulae? i can work out the wind force and the bending moment at the posts base, just not how to determine its strength etc. i can do the maths once I know the formulae
I think you’d find that wood does bend easily given the same dimensions of steel. Try finding some rebar and a wooden dowel of the same diameter and length and compare the two.
Modulus elasticity is the ratio of stress to strain of a material in deflection (say in a beam) and is sometimes called ‘Young’s modulus’.
The higher the values of Young’s modulus the better.
Units: The units are ‘Pascals’ after the late French physicist – Blaise Pascal.
And GigaPascals (GPa) are often used. For example: The Modulus elacticity of Steel is 200GPa, and some softwood timbers are around 7GPa.
Steven McColl
Structural Engineer.
“better”
I presume this means better for structural engineering?
Higher value means more stiffness – which is not necessarily better for instrument making, probably archery and whatnot if the wood needs to bend a lot.
I understand it much better now, thanks for taking the time to explain it :)
Hey, I have a question about MOR and MOE. How can it be that the MOE > MOR in some woods? How can there be less force required to break something rather than bend it?
As I understand it, comparing MOE and MOR is like comparing apples and oranges: they’re really completely different types of measurements. (A fair comparison might be to compare MOR with Crushing Strength.) MOR and crushing strength are simple measurements of the wood until failure occurs. Basically, how much force did it require to break the wood of a given size (usually standardized sizes are used). MOE is a completely different animal in that it is a RATIO of two different measurements. It’s not only the force (stress) put on the wood, but also the amount that the wood has bent… Read more »