In addition to being hygroscopic (gaining or losing moisture from the surrounding air), wood is also anisotropic. What this means is that wood has different properties depending on the direction or orientation of the grain—it’s not the same in all directions—and one of the areas where this property is most clearly seen is in dimensional shrinkage.
As opposed to a simple sponge or other isotropic material, wood (anisotropic) does not shrink in a perfectly uniform manner, and understanding this will help to avoid some pitfalls in preventing many shrinkage-related defects which may not crop up until months (or even years) after the wood product is finished.
A basic measurement of shrinkage—expressed as a percentage—is the amount that the wood shrinks when going from its green to ovendry state. In other words, since wood in its green state is at its largest dimension, and ovendry represents its driest (and therefore smallest) volume, green to ovendry is a measurement of the maximum possible percentage of shrinkage; this is referred to as the wood’s volumetric shrinkage.
Volumetric shrinkage tells how much a wood species will shrink, but it doesn’t indicate the direction of the shrinkage. The two primary planes or surfaces of wood where shrinkage takes place are across the radial plane, and across the tangential plane, corresponding to radial shrinkage, and tangential shrinkage; these two values, when combined, should roughly add up to the volumetric shrinkage.
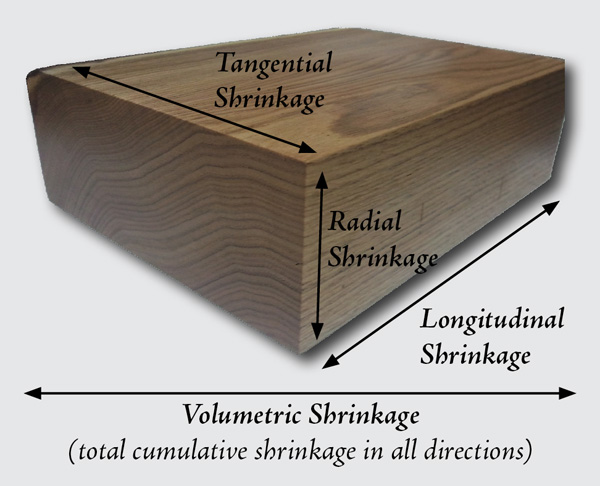
The amount a piece of wood will shrink lengthwise, called longitudinal shrinkage, is so small—typically about 0.1% to 0.2%—that it is usually inconsequential to the volumetric shrinkage. However, plywood greatly benefits from the low longitudinal shrinkage of wood—layers of wood veneer are glued together with the grain direction of each ply oriented perpendicular to the adjacent ply, which has the effect of restraining most radial or tangential shrinkage within the veneer plies. As a result, the rates of shrinkage for the width and length of a plywood panel are typically less than 1%, (though changes in thickness still remain about the same as solid wood).
Radial shrinkage in solid wood can vary from less than 2% for some of the stablest wood species, upwards to around 8% for the least stable species; most woods fall in the range of about 3% to 5% radial shrinkage. Tangential shrinkage can vary from about 3% up to around 12%; most woods fall in the range of about 6% to 10% tangential shrinkage. (Accordingly, volumetric shrinkage is typically within the range of 9% to 15% for most wood species.)
The relationship between these two shrinkage values is expressed as the tangential to radial shrinkage ratio, or simply the T/R ratio. In addition to the volumetric shrinkage, (which measures the magnitude of the shrinkage), the T/R ratio serves to measure the uniformity of the shrinkage, and is another good indicator of a wood’s stability. Ideally, a wood species with good stability would have both low volumetric shrinkage and a low T/R ratio.
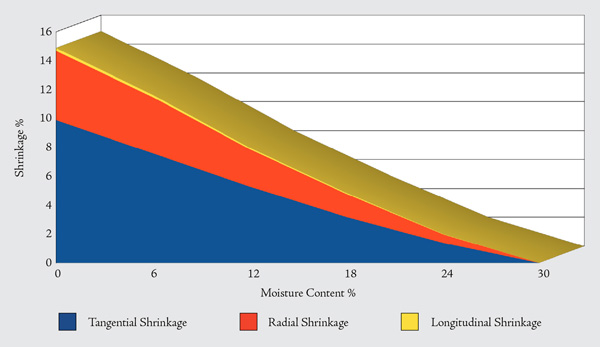 |
| A hypothetical shrinkage curve: Although shrinkage rates can vary considerably between species, (and even within the same species), this graph helps illustrate the shrinkage rates and their average proportions to one another; data was charted from values for Hard Maple (Acer saccharum), which has a T/R ratio of 2.1. Volumetric shrinkage (not pictured) is usually close to the sum of the three shrinkage percentages shown above. Tangential shrinkage accounts for the lion’s share of the overall shrinkage—about two thirds—with radial shrinkage making up most of the remaining third, and longitudinal shrinkage accounting for virtually nil. |
(It should be noted that just because a particular wood species experiences a high initial shrinkage during drying, doesn’t always correlate to an equal swelling after it has been dried. For instance, Basswood has fairly high initial shrinkage percentages—6.6% radial, 9.3% tangential, and 15.8% volumetric—yet its movement in service is relatively low. Using shrinkage and T/R ratio data simply offers woodworkers the best means of making an educated guess.)
In various wood species, the T/R ratio can range from just over 1, to nearly 3. At a T/R ratio of 1, shrinkage would occur in a perfectly uniform manner across the width and thickness of the board. At a T/R ratio of 3, the flatsawn surface would shrink or swell at triple the rate of the quartersawn surface.
As a general rule of thumb for most species, the tangential shrinkage is roughly double that of the radial shrinkage, which translates to an average T/R ratio of about 2. This helps explain why quartersawn boards are considered more stable than flatsawn boards: with quartersawn lumber, the thickness of the board is doing the majority of the shrinking or swelling, with the face of the board exhibiting minimal change in width—a useful characteristic for applications such as flooring planks or workbench tops.
Related Articles:
Get the hard copy





Is there a way to use the radial and tangential shrinkage to estimate how much a log for a log Lodge will shrink? The naive approach of just using radial shrinkage for total vertical shrinkage yields a result that is far too low – 4% in total for red oak on the attached image. Where I know there is no way that the total shrinkage which will take decades for this 2+ foot average oak is going to be 4% in diameter. I stripped the bark and sapwood last November and it has already lost about 1% diameter, and that… Read more »
If you’re using whole logs could you just use the figure for volumetric shrinkage and calculate the new log diameter with algebra and pi? It depends on what the joint is like I guess.
Thinking about it a bit more, using the value for volumetric shrinkage won’t be quite right since that would include the axial shrinkage, which should be excluded when calculating the shrinkage of the cross section of the log. However, as the article explains, axial shrinkage only constitutes 1 or 2 tenths of a percent of the total volumetric shrinkage and so could safely be ignored, although it would be easy enough to include in the calculation.
Hi, am I correct to assume that the wood species with the lowest shrinkage in every category is Hevea / Rubberwood?
No, definitely not the lowest. I’d guess something like mesquite would have among the lowest shrinkage.
Hi Eric, I recently had a pine farmhouse table custom made. They created an oak look stain but left it untreated. Now there are some significant shrinkage issues particularly on one plank. It’s winter so I have recently put the log burner on. Is it my fault or should I speak with the company who made the table or is this normal? Will the wood expand again in the future? They quote on their website that they use kiln dried wood 10-14% and to leave the table to acclimate before putting the heating on. How long is a reasonable amount… Read more »
I guess it depends on just how dry the farmhouse got. Do you have a way to measure ambient relative humidity? I’d say if it’s below maybe 20 or 30% RH, that would be very dry and perhaps an unusually dry location that would require special consideration.
The gaps may close up a bit in more humid weather, but I doubt they will ever completely disappear. It wouldn’t matter too much how long you acclimatize the table for beforehand if the heater caused the humidity level to drop very quickly.
Hi Derek,
Many thanks for your reply.
I don’t have a way to measure humidity right now but I will certainly source something soon and I do have a humidifier running now also.
The look of the cracks themselves don’t bother me a great deal as I do like a rustic look. But I’m worried about the structural integrity of the wood? Is it possible it would crack all the way through?
Thank you.
I really don’t think it should be much of a concern structurally. More than likely they are surface checks from rapid change in moisture level.
If the first shrinkage value is 25%, then it swells back to its original dimensions; what would the shrinkage value you obtain for 2nd time shrinkage be?Increase or decrease? Why?
Generally, the first time the wood shrinks it is greater than subsequent times, and the drier it gets initially, the lesser the subsequent shrinkage will be, to an extent. Of course every species is different, and there’s a lot of gray areas in these types of measurements, so I tend to only report green to ovendry shrinkage numbers. But I know many Australian sources will list both initial shrinkage and also a “seasoned” shrinkage number too.
I’m looking for something on the site to tell me how to use the shrinkage percentages to calculate what they are on a per inch basis. I’m building a cabinet made of 4/4 by 14 inch thick Lati boards, where the end grain is slanted at about 30 to 40 degrees to the face, which have no flat grain. Would I use the tangential or radial percentage for the width, or split the difference? Do I just multiply the percentage times the width, i.e using 10.6% tangential shrinkage figure means .106 x 14 inches = about 1 1/2 inches movement?… Read more »
The shrinkage numbers represent the total amount of change from green to oven dry. So your calculations would be correct if you theoretically had a board that was green and completely undried (very unlikely for most people) and then you dried it all the way down to 0% moisture (again, almost impossible in most instances). In real-world situations, it’s a little complicated to calculate things exactly since technically shrinkage doesn’t happen in a perfectly linear fashion. But in general, to get a decent ballpark estimate, it works best to assume a fiber saturation point of about 28% moisture content. So… Read more »
a bought a signa wood table last month. no the wood strips have come apart, and the manufacturer said this has happened because the wood shrunk do to not being treated? ca it shrink so quickly from not being treated for 5 weeks?
Fully drying takes a long time, but yes wood that isn’t sealed can shrink enough to crack in a few days if the change in humidity is enough. Green wood can develop cracks in a few minutes if it’s wet enough.
I recently purchased a couple of 4 x 4s for the legs of a workbench. The moisture measured 12%, and I wrote daily measurements on the surface for a couple of weeks, and they settled at 10%.
I cut them into 36″ pieces, and within 2 days saw small shrinkage cracks forming on the ends. Given the use, not a major issue, but I sealed the ends with shellac and shrinkage stopped.
Hi Eric, I’m making a table using a rosewood slab 2” thick and about 14” wide. Do I need to worry about tangential expansion/shrinking? I’m considering framing it with 1 1/2” mitered corners using hard maple.
Thanks in advance,
Mike
I would not recommend using mitered corners for a solid wood table of any wood species as it would be asking for trouble. You could glue straight strips of maple along the side parallel to the grain and then do breadboard ends in maple to achieve a similar framed appearance.
Hi Eric, I’m having a hornbeam felled and cut into rounds which I then need to season. Each round will eventually be milled on my CNC router down to 0.918”. I will use the rounds to make wood type, the letters being cut into the end grain. My question is, how thick should I have the rounds cut after the tree is felled? I don’t imagine there’ll be much longitudinal shrinkage as that dimension will a little over an inch. Are the rounds likely to warp do you know? Finally, how long should I season the rounds for? Given that… Read more »
Drying time will depend a lot on thickness of each disk. I’d just use your best judgment on thickness on what seems reasonable for your application. But I’d cut them first, then weight a few on a small postage scale or something similar, and then you can just keep track of the weight every few days (or weeks) and see how long it takes for the weight to come down to a stable level. I’d imagine if each round is less than an inch thick it should be less than a month, but that’s only a ballpark guess, it may… Read more »
Thanks very much, Eric.
Hi, Eric! I hope you still read/reply to comments on old posts. I have a special request… would you please help me out with a recommendation for a rather unique project? I’d like to try making some reference quality metric setup blocks out of wood (they’re normally made from brass https://bit.ly/3gxlTov for stability). I haven’t been able to find a source for metric setup blocks. I’m sure I could have some machined but I’m an avid DEYer (Do Everything Yourself) and besides, this would be a labor of love. Anyway, to do this, I’ll have to cut the blocks a… Read more »
Which dimension in the wood are you referencing when you give the 1″ measurement? Length is much less than width or height.
I’d consider mesquite (Prosopis species) as a good fist pic, as they are known to be rather stable and resistant to movement with changes in humidity — not to mention pretty hard. Otherwise, a lot of rosewoods can be stable and are hard. Mopane or padauk might be other woods to consider.
The height and width would be 25mm. (And another one that’s 2mm, 3mm, 4mm, 6mm, 12mm, etc.)
Thanks for the recommendations!
Looking for information on how much douglas fir heartwood shrinks, for the purpose of a log cabin build where I cut most of the sapwood off the log. I want to know if I need to dry the logs or if I can stack them right away with zero gap.
Can I ask, please. Would green oak be suitable for a plank table in a conservatory. Obviously it’s quite a damp atmosphere especially in the winter months, but it’s hot and damp in the summer months. A suitable oak fell in the last storm and I wondered if it could replace the veneered planks on the two tables I have in my conservatory. Grateful for some advice!
Hard to say for sure without knowing more details of width of planks, MC of wood, etc. Generally, you’d want to avoid directly using green wood for most projects, and allow planks to reach EMC first, especially before final jointing/planing.
Thank you so much Eric. I’ve done a little more digging and one of the reasons I asked is that if you could use it green I’d get it much sooner! Yes, boredom during Covid is a problem here! The lengths will be 2 meters, with 30cm and depth is 3 cm. I do have a local timber merchant who can kiln dry it for me. The other reason is that we have offered 2 oaks for the rebuilding of Notre Dame in the name of our 4 French grandchildren and that apparently has to be green although it’s not… Read more »
I felt like a bum for using this site so often so I bought the book. It’s great but when I Google a question about wood, I’m often brought here again.
If I’m working with 2 x 8 pressure treated lumber measuring 7 1/2″ and the wood has a moisture content of 20% what can I expect the lumber to measure after it has dried out? Thank you!
I made a mistake. The moisture ranges anywhere from 30 to 50% on these new boards with an average rating of near 35%. I was told that they were kiln dried before treatment.
I’m expecting the lumber to dry to somewhere near 9%. Thank you.
I want to build a guitar neck from a quarter-sawn piece of lumber. For shrinkage of the finished neck due to changing humidity, I primarily care about the change in the length of neck, since that is what affects the pitch of the strings.
Is there any source of data for longitudinal shrinkage of various species?
The shrinkage in length is inconsequential with respect to fingerboard length. The 0.1% quoted above is for volumetric shrinkage from green. The wood you’ll be using for an instrument should be dried to about 6 or 7% moisture content. The seasonal dimensional changes in length of dry wood will be only a very tiny fraction of the 0.1% stated in the article.
Should longitudinal shrinkage be accounted for in furniture making? Example?
Hi, I’m Interested in wood with similar shrinking properties, specifically, mahogany and anything else that is way less expensive that I can use in conjunctiin with mahogany. I have a huge project going on and Id like to mate different species in various capacities where the magogany will be showing and the cheaper would would never be visible. This would enabke me to use much less mahogany than if I used solid pieces and I could not only cut the cost way down, but would also have an easier time sourcing material if using less actual mahogany. This all depends… Read more »
You didn’t mention if it also had to be similar hardness/toughness. Yellow poplar is a cheap wood with pretty good stability, though you wouldn’t necessarily see that from it’s volumetric shrinkage number. Another choice might be red alder. All this would be dependent on finding clear and quality boards that don’t have any knots. Also, you may want to seriously consider mahogany veneer instead.
“volumetric shrinkage is essentially equal to the sum of the three shrinkage percentages shown above” — would it not be the product? v = wxbxh?
Yes, but since the percents are all very close to one, adding them is a close approximation. So take a board with shrikages of 8%, 4%, and 1%. The volume will be .92 * .96 * .99 = .874368, or 12.5632% overall shrinkage. That’s very close to the 13% you’d get from summing the percents.
In practice, the error you get from this approximation will be swamped by the variation between different pieces of wood. So it’s a safe “close enough” rule to use.
This site gives radial Rs, tangential Ts, and volumetric Vs shrinkage. To calculate length shrinkage from green to dry:
Ls = 1 – (1-Vs) / ((1-Rs) * (1-Ts))
where, for example, 8.2% would be entered as 0.082.
For example, for Western White Pine, volume shrink is 11.8%, radial shrink is 4.1%, and tangential shrink is 7.4%. So longitudinal shrink is:
Ls = 1 – (1-0.118) / ((1-0.041) * (1-0.074)) = 0.0068, or 0.68%.
There are some cases where Ls comes out negative. This is not possible, so take the numbers as approximations.
Actually, while this should be correct in theory, it’s more or less wrong in practice. That’s because each variable may be tested and recorded a different number of times, and from different sources/trees. Say, for instance, you have a rift sawn piece of wood with grain at an 45 degree angle. You couldn’t really use a piece like this to accurately measure radial OR tangential shrinkage, but you could use it to measure overall volumetric shrinkage. What this ultimately results in is a greater number of samples being tested for volumetric shrinkage, as well as a slight discrepancy between the… Read more »
Strategies for furniture joinery: https://www.extension.purdue.edu/extmedia/FNR/FNR-163.pdf
Numbers for wood: https://www.fpl.fs.usda.gov/documnts/pdf1957/peck57a.pdf
Many thanks for sharing the shortcuts. I have been wondering about the best way to attach a solid wood table top to its support rails to allow for its shrinkage/swells and the first paper has given me a few suggestions. Good papers to read for anyone who is interested in wood or woodworking.
I have a simple question, I have made some white pine table tops that in the middle of winter split up the middle , ussaly when the table had opposite direction grain end boards at each end . I am assuming this was a result of my lack of ensuring the wood was 6-8% mc. I think if I keep the wood low in numbers like 6% or even 5.5 % mc and seal it with extra lacquer that it will handle the dry winter inside a home ? Or should I not use end boards , or switch to… Read more »
Will freshly milled dimensional eastern red cedar shrink and expand greatly in the first couple of months it is laid down. Having a slow start and wondering about tight fitting on later boards.
I’m wondering how a wood species’ T/R ratio relates, if at all, to its tendency to check, especially in large boxed heart beams. Here are my hypotheses. I noticed that eastern white pine, even though it has very low shrinkage numbers, has a very high T/R ratio, and I’ve read elsewhere that it checks more than other species, so that makes me think higher T/R ratios would be associated with more checking. With a boxed heart beam it would seem like checking would normally be the result of wood shrinking faster tangentially than it shrinks radially, but since the circumference… Read more »
I can offer some insight from a scientific perspective. In order to help understand, lets consider what causes checks. Checking occurs when the forces acting upon the wood exceed the tensile strength causing the wood fibers to pull apart and resulting in cracks. Also notice that these happen running parallel with the grain, which suggests that the forces are acting perpendicular to the grain. As to your first question, the higher the T/R ratio the more the relative amount of tangential shrinkage occurs. Both these shrinkages happen at right angles to the grain. As the T/R ratio gets closer to… Read more »
WE ARE HAVING ISSUES IN SHRINKAGE. WE USE CHIP CORE AND WE GLUE A SOLID WOOD PIECE AROUND THE PERIMETER. HOW MUCH MOISTURE VARIANCE SHOULD THERE BE BETWEEN THE TWO SUBSTRATES ?
We have problems of swelling in Oak Glulam furniture doors made by Venjakob, the door is only 688mm high and has swelled by 8mm, the relative humidity range of the room is between 45-55% and the temperature range is between 18 – 22 deg. The glue laminated timber runs horizontally and the door thickness is 20mm. Can you please advise what your assessment of the problem is.
what was the moisute content of the wood during production of the furniture? It should be between 6-8% otherwise it may cause problems as described
We had hardwoods installed throughout (except bath and kitchen). In the hall the wood is laid perpendicular to the hall and terminates in the foyer. This is where the directionality changes as the foyer is laid parallel to the hall so the wood meets sort of T shaped.Very easily a quarter could be dropped in the winter gap. I’d guess it is easily 1/8″. However, at the other side of the foyer is the dining room and the direction of the planks is identical to the foyer. At the end of the dining room is the kitchen. The gap at… Read more »
you need to find a way to control the humidity in your house. the change in gaps between boards are from a change in the humidity.
Im getting ready to cut down a large pecan and cedar tree. I plan to slab both for table top projects. If I want a finished 3″ thickness, how thick do I have to cut it green? Does the book cover this type of info?
Wood this be mostly for quartersawn lumber? Or do plainsawn and rift sawn shrink in the same manner?
Quartersawn lumber tends to shrink/expand more in it’s thickness, and not as much in its width (dependent upon the wood’s T/R ratio). Plainsawn is just the opposite, and is the least stable, shrinking most along the width of the board, and least in thickness. Adding to its instability is the fact that most plainsawn boards do not have perfectly horizontal grain, but tend to have a varying pitch to the grain, edging more towards rift or even quartersawn (vertical grain) towards the edges of the board.